O disco de 12 kg tem uma velocidade angular . Se o freio ABC é aplicado de tal que a intensidade da força P varia com o tempo, como mostrado, determine o tempo necessário para parar o disco. O coeficiente de atrito cinético em B é . Despreze a espessura do freio.
Passo 1
Para resolver esse exercício, iremos considerar a aceleração da gravidade .
Começaremos o exercício notando que há presença de força de atrito cinético em B para poder parar o disco, e ela é dada por:
Com isso, é possível aplicar o somatório de momento em torno do ponto A com o auxílio da figura a seguir e obter uma relação entre e P:
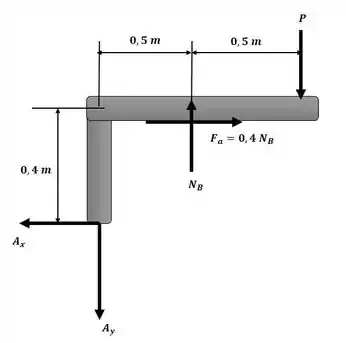
Sendo assim, substituindo esse valor na primeira equação obtida no passo 1, é possível encontrar também a força de atrito em função de P:
Passo 2
Agora, antes de aplicaremos o princípio do impulso e do momento angular em torno do ponto O, devemos encontrar o momento de inércia do cilindro, sendo assim:
Com isso, agora podemos aplicar o princípio do impulso e do momento angular em torno do ponto O com o auxílio da imagem a seguir:
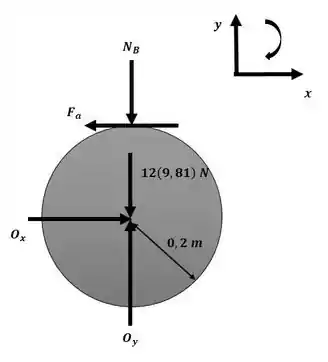
Essa será nossa equação 1. No entanto, sabemos do cálculo, que a integral de uma função estritamento positiva equivale a área sob a curva dessa mesma função, dessa forma, considerando t > 2 s (pois ainda não sabemos o tempo de parada):
Essa será nossa equação número 2.
Passo 3
Agora podemos substituir o valor da integral encontrado na equação 2 na nossa equação 1, sendo assim:
E, resolvendo para t: